http://www.youtube.com/watch?v=mvj_KLgO_5Q
Una función es una relación entre dos variables, de forma que a cada valor de la variable independiente , le asocia un único valor de la variable dependiente
, le asocia un único valor de la variable dependiente  , que llamaremos imagen de
, que llamaremos imagen de  . Decimos que y es función de
. Decimos que y es función de  y lo representamos por
y lo representamos por
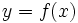

Una función es una relación entre dos variables, de forma que a cada valor de la variable independiente
 , le asocia un único valor de la variable dependiente
, le asocia un único valor de la variable dependiente  , que llamaremos imagen de
, que llamaremos imagen de  . Decimos que y es función de
. Decimos que y es función de  y lo representamos por
y lo representamos por 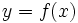
Propiedades
- Dominio :

- Recorrido :

- FUNCIONES SIMÉTRICAS
Simetría respecto del origen de coordenadas O(0,0)
Una función f es simétrica respecto del origen cuando para todo x del dominio se tiene
y se denominan funciones impares.
Simetría respecto del eje de ordenadas OY
Una función f es simétrica respecto del eje de ordenadas cuando para todo x del dominio se tiene
y se denominan funciones pares.
Simetría respecto del eje de abscisas OX
Dos funciones f y g son simétricas respecto del eje de abscisas si son funciones opuestas, es decir
Simetría respecto de la bisectriz del 1º y 3º cuadrante
Dos funciones f y g son simétricas respecto de la bisectriz del 1º y 3º cuadrante si son funciones recíprocas, es decir
La gráfica de una función par (impar) queda determinada si conocemos su forma para valores positivos de x , ya que la parte de la gráfica correspondiente a valores negativos de x se construye por simetría respecto del eje de ordenadas.
- FUNCIONES PERIÓDICAS
Una función f es periódica de periodo T si
para todo x perteneciente al dominio de definición.
Las funciones periódicas más importantes son las funciones circulares seno, coseno y tangente.
- CONTINUIDAD
Una función es continua en un punto si existe límite en dicho punto y coincide con el valor que toma la función en ese punto.Tipos:


 .
.













